Herschel-Quincke管
Herschel-Quincke管
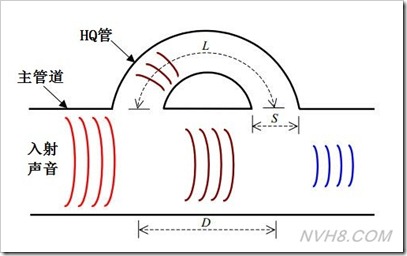
Herschel-Quincke Tube,中文译为赫歇尔-昆克管,简称HQ管,也称之为1/2波长管。其形状如下图所示,HQ管也是消声元件的一种。Herschel在1833年首次提出了HQ管的声学理论设想,即当声音沿着一个管进入并穿过两个不同长度的管道(两管道的长度差为声波波长整奇数倍),一路继续在主管传播,另外一路沿着支管传播,声波在管系下游交汇处相遇,因反相干涉现象会使得声音减弱或消失;Quincke由1886年用实验验证了Herschel设想的正确性,因此该消声元件也就被正式命名为Herschel-Quincke管。
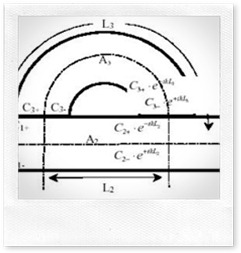
Herschel-Quincke管声学计算:
HQ管有两个消声频率,一个是由两管长度之差引起的消声频率,一个是由两管之和引起的消声频率
,其计算公式如下所示:
;
因此也是称HQ管为1/2波长管的由来,其传递损失计算公式如下:
其中:
;
;
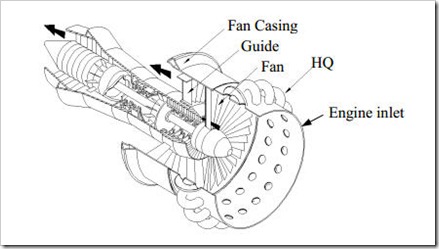
HQ管消声结构简单,尽管消声频段窄但是消声效果非常显著,因此已经被大量应用于航空、航天领域,如下图所示就是一个被应用于涡轮发动机的HQ消声装置。而在汽车NVH领域则主要应于与发动机进气系统的声学控制。
 |
|
图片来源:Lib.vt.edu |
更多NVH相关术语解释参见: NVH百科
本文地址:https://nvh8.com/343.html
Copyright© NVH吧 欢迎转载,但转载时请以链接形式注明作者和原始出处,谢谢!