NVH吧

窗函数

窗函数，英文Window Function，是一种除在给定区间之外取值均为0的实函数，主要应用在频谱分析、波束形成、滤波器设计等信号处理中。现代数字信号处理的主要工具是傅里叶变换，而快速傅里叶变换假定时间信号是周期无限的。在实际工程测试处理时不可能对无限长的信号进行测量和运算，，往往只截取有限的时间片段进行分析，当无限长的信号被截断后，其频谱发生了畸变，出现频谱能量泄漏状况，而为了减少频谱能量泄漏，可采用不同的截取函数对信号进行截断，这种截断函数即称之为窗函数，简称为窗。

典型的窗函数

实际应用的窗函数，基本可以分为如下几个类型：

1、幂窗函数

采用时间变量某种幂次的函数，如矩形、三角形、梯形或其他时间(t)的高次幂的窗函数

(1) 矩形窗 – Rectangular Window

矩形窗是一种最简单的窗函数，属于时间变量的零次幂窗。矩形窗使用最多,习惯上不加窗就是使信号通过了矩形窗。这种窗的优点是主瓣比较集中,缺点是旁瓣较高，并有负旁瓣,导致变换中带进了高频干扰和泄漏，甚至出现负谱现象。

矩形窗计算公式如下：

(2) 三角窗 (或巴特利特 Bartlett 窗)

三角窗是幂窗的一次方形式，是由Bartlett提出的一种逐渐过渡的三角窗形式。与矩形窗比较，主瓣宽约等于矩形窗的两倍，但旁瓣小，而且无负旁瓣。

三角窗计算公式如下：

2. 三角函数窗

应用三角函数，即正弦或余弦函数等组合而成的复合函数窗，例如汉宁窗、哈明窗等

(1) 汉宁窗 – Hanning Window

汉宁窗又称升余弦窗，汉宁窗可以看作是3个矩形时间窗的频谱之和，或者说是 3个 sinc（t）。

汉宁窗计算公式如下：

(2)哈明窗 – Hamming Window

型函数之和，而括号中的两项相对于第一个谱窗向左、右各移动了 π/T，从而使旁瓣互相抵消，消去高频干扰和漏能。可以看出，汉宁窗主瓣加宽并降低，旁瓣则显著减小，从减小泄漏观点出发，汉宁窗优于矩形窗．但汉宁窗主瓣加宽，相当于分析带宽加宽，频率分辨力下降。

哈明窗计算公式如下：

3. 指数窗

采用指数时间函数的窗函数，如高斯窗等

高斯窗 – Gaussian window

高斯窗是一种指数窗。高斯窗谱无负的旁瓣，第一旁瓣衰减达一55dB。高斯富谱的主瓣较宽，故而频率分辨力低．高斯窗函数常被用来截短一些非周期信号，如指数衰减信号等。

高斯窗计算公式如下：

除此此外，还有Papoulis窗、Parzen窗、Poisson窗、Cauchy窗、Bartlett-Hann、Blackman-Harris 、 Nuttall’s Blackman-Harris 、 Bohman 、 Flat Top window 、 Hann 、 Parzen (de la Valle-Poussin ) 、 Tapered cosine 等等。

窗函数的选择

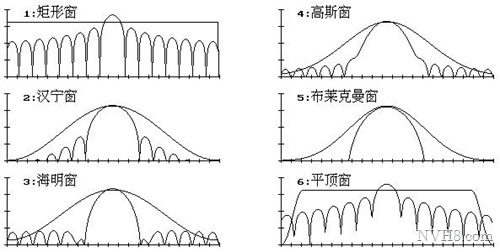
上图所示为常见的几种窗函数的 时域和频域波形。对于窗函数的选择，应考虑被分析信号的性质与处理要求。如果仅要求精确读出主瓣频率，而不考虑幅值精度，则可选用主瓣宽度比较窄而便于分辨的矩形窗，例如测量物体的自振频率等；如果分析窄带信号，且有较强的干扰噪声，则应选用旁瓣幅度小的窗函数，如汉宁窗、三角窗等；对于随时间按指数衰减的函数，可采用指数窗来提高信噪比。

参考：

• 1. http://en.wikipedia.org/wiki/Window_function
• 2. http://baike.baidu.com/view/2327611.htm
• 3. http://netclass.csu.edu.cn/NCourse/hep028/java_hls/gccs/windowf.htm
• 4. http://jpkc.jwc.bupt.cn:4213/szxhcl/course/cbook/%E7%AC%AC%E4%BA%94%E7%AB%A0/5_2_4.html

更多NVH相关术语解释参见：NVH术语大全